Podejmowanie decyzji przy wielości kryteriów
Optymalizacja wielocelowa to dział badań operacyjnych, zajmujący się wyznaczeniem optymalnej decyzji w przypadku, gdy występuje więcej niż jedno kryterium oceny.
Wielocelowe zadanie decyzyjne (WZD) można zapisać w następującej postaci:
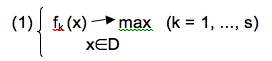
gdzie: x – dowolne rozwiązanie (decyzja)
fk(x) – funkcja celu związana z k – tym kryterium cząstkowym
D – zbiór dopuszczalnych rozwiązań (decyzji)
Jak to obliczyć?
W przypadku wielu celów ocena, która z dwóch decyzji jest lepsza, a tym samym wybór decyzji najlepszy, czyli optymalnej ze względu na wszystkie kryteria, jest sprawą bardzo trudną. Załóżmy, że mamy dwa kryteria oceny f1(x) i f2(x) (obydwa na maksimum oraz dwie decyzje x’ i x’’, dla których:
f1(x’) = 10 > f2(x’’) =6,
f2(x’) = 30 < f2(x’’) = 42.
Biorąc pod uwagę funkcję celu f1 wyżej oceniamy decyzję x’ niż decyzję x’’. Ze względu na funkcję celu f2 lepsza jest decyzja x’’ niż x’. Która z nich jest lepsza, jeżeli musimy brać pod uwagę obydwie funkcję? Trudno nam na to pytanie odpowiedzieć. Musimy na nowo zdefiniować pojęcie rozwiązania optymalnego w przypadku wielości celów jest. Jednym ze sposobów wyznaczania najlepszej decyzji w wawunkach wielu celów jest szukanie rozwiązania optymalnego w sensie Pareto
Def.
Rozwiązaniem optymalnym w sensie Pareto nazywamy takie rozwiązanie x’, że nie istnieje żadne rozwiązanie x∈D dające poprawę wartości chociaż jednej funkcji celu, nie powodując pogorszenia wartości innych funkcji celu. Rozwiązanie optymalne w sensie Pareto często nazywa się rozwiązaniem sprawnym lub efektywnym.
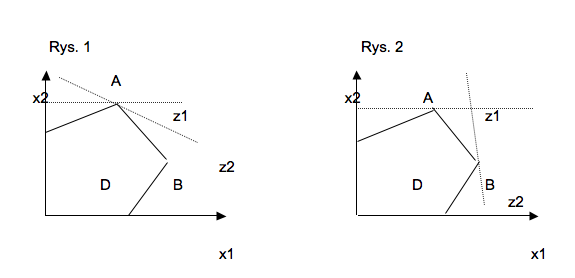
Niestety, na ogół rozwiązań optymalnych w sensie Pareto jest wiele. Jedno rozwiązanie optymalne w sensie Pareto występuje wówczas, gdy wszystkie optima cząstkowe znajdują się w tym samym punkcie. Ten przypadek pokazuje rys. 1. W sytuacji pokazanej na rys. 2 każda funkcja celu ma inne rozwiązania optymalne,
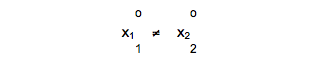
Więc rozwiązaniem optymalnym w sensie Pareto jest każdy punkt na odcinku AB.
W skrajnej sytuacji każde rozwiązanie dopuszczalne może być rozwiązaniem sprawnym. Powstaje pytanie, jak spośród wielu rozwiązań (optymalnych w sensie Pareto) wybrać jedno rozwiąznanie kompromisowe?
Istnieje wiele takich propozycji. Zależą one od dodatkowych preferencji wyrażanych przez decydenta wobec kryteriów. Oto niektóre propozycje.
a) Metakryterium
Metakryterium to funkcja określona na kryteriach cząstkowych. Podaje ona użyteczność poszczególnych decyzji dla decydenta:
U(x) = u[f1(x), f2(x), …,fs(x)].
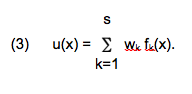
Rozwiązanie zadania sprowadza się do znalezienia w zbiorze rozwiązań dopuszczalnych decyzji najlepszej w sensie metakryterium u(x). Decyzja najlepsza w sensie u(x) jest poszukiwaną decyzją kompromisową.
B) Jedno kryterium główne, pozostałe drugorzędne
Niekiedy decydent stwierdza, że jedno kryterium jest zasadnicze (główne), a pozostałe są mniej istotne (drugorzędne). Szukamy wówczas decyzji najlepszej w sensie kryterium głównego, ale jednocześnie takiej, która zapewnia określony poziom realizacji kryteriów drugorzędnych.
Aby wyznaczyć decyzję kompromisową formułujemy zadanie
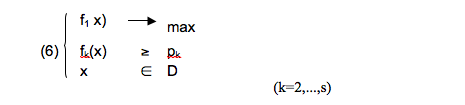
gdzie f1 – kryterium główne,
pk – zadawalający poziom realizacji k – tego kryterium drugorzędnego.
C) Ścisła hierarchia celów
Jest to uporządkowanie wszystkich kryteriów od najważniejszego do najmniej ważnego. Przy wyznaczaniu rozwiązania kompromisowego, nie przekroczy się ustalonego odstępstwa od maksymalnych wartości poszczególnych kryteriów.
Przyjmijmy że kryterium o niższym numerze jest ważniejsze od kryterium o numerze wyższym. Współczynnik odstępstwa dla danego kryterium oznaczamy przez
dk (0 ≤ dk ≤ 1 dla k = 1,…, s-1)
Rozwiązujemy ciąg zadań pomocniczych Lk (k=1,…,s).Rozwiązanie końcowego zadania Ls wyznacza decyzję kompromisową zadania wielocelowego.
D) Minimalizacja odległości od punktu idealnego.
W przypadku, gdy nie ma żadnych preferencji dla poszczególnych kryteriów cząstkowych, jako rozwiązanie kompromisowe wybieramy punkt leżący najbliżej punktu idealnego.

