Rodzaje liczb w matematyce są kluczowym elementem, który pozwala na zrozumienie różnych aspektów tej dziedziny. W matematyce liczby dzielą się na wiele kategorii, które odzwierciedlają ich właściwości i zastosowania w praktyce. Poznanie tych rodzajów liczb, takich jak liczby naturalne, całkowite, wymierne czy niewymierne, jest niezbędne dla każdego, kto chce zgłębić tajniki matematyki oraz jej zastosowanie w codziennym życiu.
W artykule przyjrzymy się szczegółowo każdemu z rodzajów liczb, ich definicjom oraz zastosowaniom. Dowiemy się, jak liczby naturalne służą do liczenia, jak liczby całkowite obejmują również wartości ujemne, a także jakie znaczenie mają liczby wymierne i niewymierne w różnych dziedzinach nauki. Zrozumienie tych podstawowych koncepcji jest fundamentem dla dalszej nauki matematyki.
Najistotniejsze informacje:
- Liczby naturalne to liczby używane do liczenia, zaczynające się od 1.
- Liczby całkowite obejmują liczby naturalne, ich przeciwne oraz zero.
- Liczby wymierne to liczby, które można przedstawić jako ułamek.
- Liczby niewymierne nie mogą być zapisane jako ułamek i mają nieskończone rozwinięcie dziesiętne.
- Liczby zespolone mają formę x + iy i są używane w bardziej zaawansowanych obliczeniach matematycznych.
- Liczby pierwsze to liczby naturalne większe od 1, które mają dokładnie dwa dzielniki.
- Liczby doskonałe to liczby, których suma dzielników właściwych równa się samej liczbie.
- Ciąg Fibonacciego to sekwencja liczb, w której każda liczba jest sumą dwóch poprzednich.
Rodzaje liczb w matematyce i ich podstawowe definicje
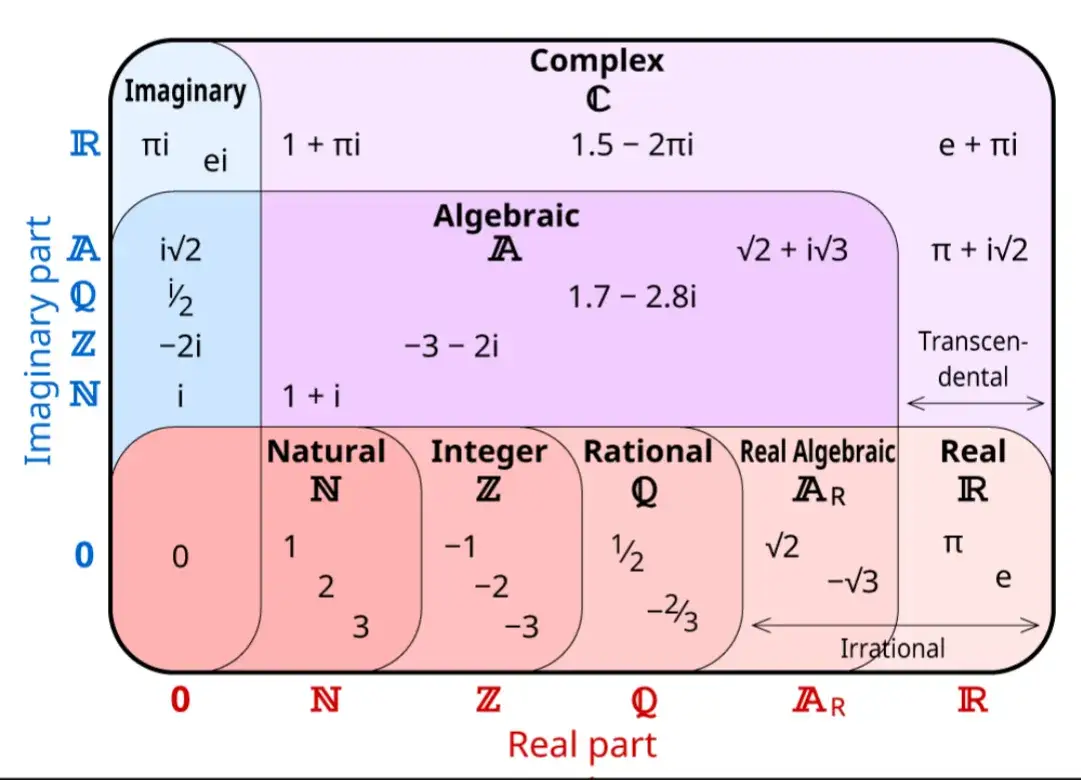
W matematyce liczby dzielą się na różne rodzaje, które tworzą hierarchię zgodnie z ich właściwościami i zastosowaniami. Najważniejsze z nich to liczby naturalne oraz całkowite. Liczby naturalne, które zaczynają się od 1, są podstawą wszelkich obliczeń i służą do liczenia oraz porządkowania. W niektórych kontekstach obejmują także zero, co czyni je bardziej uniwersalnymi.
Liczby całkowite to szersza kategoria, która obejmuje liczby naturalne, ich przeciwne oraz zero. Oznacza to, że liczby całkowite mogą być zarówno dodatnie, jak i ujemne, co jest istotne w różnych zastosowaniach, takich jak reprezentacja wartości ujemnych, na przykład w pomiarach temperatury czy saldo finansowe. Zrozumienie tych podstawowych rodzajów liczb jest kluczowe dla dalszej nauki matematyki i jej zastosowań w codziennym życiu.
Liczby naturalne - klucz do zrozumienia matematyki
Liczby naturalne to liczby, które zaczynają się od 1 i są używane głównie do liczenia i porządkowania. Przykłady to 1, 2, 3, 4, 5 i tak dalej. W praktyce, liczby naturalne są fundamentem matematyki, ponieważ pozwalają na określenie ilości rzeczy, takich jak liczba jabłek w koszyku czy liczba uczniów w klasie. Są one niezbędne do zrozumienia bardziej skomplikowanych koncepcji matematycznych.
Liczby całkowite - jak obejmują liczby ujemne i zero
Liczby całkowite to zbiór liczb, który obejmuje zarówno liczby naturalne, jak i ich przeciwności, w tym zero. Oznacza to, że liczby całkowite zawierają wartości dodatnie, ujemne oraz zero, co czyni je niezwykle ważnymi w matematyce. Przykłady liczb całkowitych to: -3, -2, -1, 0, 1, 2, 3. Dzięki tej różnorodności, liczby całkowite są używane do reprezentowania różnych scenariuszy, takich jak pomiar temperatury, saldo finansowe czy położenie geograficzne.
W praktyce, liczby całkowite pozwalają na łatwe porównywanie wartości. Na przykład, w kontekście finansowym, saldo -50 zł oznacza, że mamy dług, podczas gdy saldo +50 zł oznacza, że posiadamy oszczędności. Zrozumienie liczb całkowitych jest kluczowe dla dalszego zgłębiania bardziej skomplikowanych koncepcji matematycznych oraz ich zastosowań w życiu codziennym.
Klasyfikacja liczb - zrozumienie ich właściwości i zastosowań
W matematyce istnieje wiele klasyfikacji liczb, które pomagają zrozumieć ich właściwości oraz zastosowania. Główne kategorie to liczby wymierne i niewymierne. Liczby wymierne to takie, które można zapisać jako ułamek, na przykład 1/2 lub 0,75. Z kolei liczby niewymierne, takie jak π czy √2, nie mogą być przedstawione w formie ułamka, co sprawia, że mają nieskończone rozwinięcie dziesiętne.
Klasyfikacja liczb jest istotna, ponieważ umożliwia lepsze zrozumienie, jak różne rodzaje liczb współdziałają ze sobą w różnych kontekstach matematycznych. Na przykład, liczby wymierne są powszechnie stosowane w obliczeniach finansowych, natomiast liczby niewymierne często pojawiają się w geometrii i analizie matematycznej. Zrozumienie tych klasyfikacji jest kluczowe dla każdego, kto chce zgłębić temat rodzajów liczb w matematyce.
Liczby wymierne - ułamki i ich praktyczne zastosowania
Liczby wymierne to liczby, które można przedstawić jako ułamek w postaci $$\frac{a}{b}$$, gdzie $$a$$ i $$b$$ są liczbami całkowitymi, a $$b \neq 0$$. Oznacza to, że każda liczba wymierna może być zapisana w formie ułamka, co czyni je niezwykle użytecznymi w codziennym życiu. Przykłady liczb wymiernych to 1/2, 3/4 czy 0,75. Dzięki tej elastyczności, liczby wymierne są podstawą wielu obliczeń w matematyce oraz różnych dziedzinach nauki.
Praktyczne zastosowania liczb wymiernych są szerokie. W finansach, na przykład, często posługujemy się ułamkami do obliczania odsetek lub dzielenia kosztów. W kuchni, przepisy często wymagają użycia ułamków, aby precyzyjnie określić ilości składników. Liczby wymierne są również kluczowe w naukach przyrodniczych, gdzie precyzyjne pomiary są niezbędne. Poniżej znajduje się tabela porównawcza najpopularniejszych ułamków i ich odpowiedników dziesiętnych.
| Ułamek | Odpowiednik dziesiętny |
| 1/2 | 0,5 |
| 3/4 | 0,75 |
| 2/5 | 0,4 |
| 5/8 | 0,625 |
Liczby niewymierne - ich znaczenie w matematyce i naukach
Liczby niewymierne to liczby, które nie mogą być zapisane jako ułamek dwóch liczb całkowitych. Mają one rozwinięcie dziesiętne nieskończone i nieokresowe. Przykładami liczb niewymiernych są liczba π (pi) oraz √2. Liczby te odgrywają kluczową rolę w matematyce, zwłaszcza w geometrii i analizie matematycznej, gdzie często pojawiają się w obliczeniach związanych z kątami, długościami oraz objętościami.
Czytaj więcej: Jak się mnoży logarytmy - proste zasady i najczęstsze błędy
Liczby zespolone - wprowadzenie do bardziej zaawansowanej matematyki
Liczby zespolone to liczby, które mają postać $$x + iy$$, gdzie $$x$$ i $$y$$ są liczbami rzeczywistymi, a $$i$$ to jednostka urojona, spełniająca warunek $$i^2 = -1$$. Liczby zespolone są kluczowe w bardziej zaawansowanej matematyce, ponieważ pozwalają na rozwiązanie równań, które nie mają rozwiązań w zbiorze liczb rzeczywistych. Na przykład, równanie $$x^2 + 1 = 0$$ nie ma rozwiązań w zbiorze liczb rzeczywistych, ale w zbiorze liczb zespolonych ma dwa rozwiązania: $$i$$ i $$-i$$. Dzięki tym właściwościom, liczby zespolone są niezwykle ważne w różnych dziedzinach matematyki oraz nauk ścisłych.
Zastosowania liczb zespolonych w różnych dziedzinach
Liczby zespolone znajdują zastosowanie w wielu dziedzinach, w tym w inżynierii, fizyce oraz teorii sygnałów. W inżynierii elektrycznej, na przykład, liczby zespolone są używane do analizy obwodów prądu zmiennego, gdzie pozwalają na łatwiejsze obliczenia związane z impedancją. W fizyce, liczby zespolone są wykorzystywane w mechanice kwantowej do opisu stanów cząstek. Dodatkowo, w teorii sygnałów, liczby zespolone są niezbędne do analizy sygnałów w dziedzinie częstotliwości.
- Inżynieria elektryczna - analiza obwodów prądu zmiennego
- Fizyka - opisywanie stanów cząstek w mechanice kwantowej
- Teoria sygnałów - analiza sygnałów w dziedzinie częstotliwości
Liczby pierwsze i złożone - ich rola w teorii liczb
Liczby pierwsze to liczby naturalne większe od 1, które mają dokładnie dwa dzielniki: 1 oraz siebie samą. Przykłady liczb pierwszych to 2, 3, 5, 7, 11 i 13. Z kolei liczby złożone to liczby, które mają więcej niż dwa dzielniki, co oznacza, że można je podzielić przez inne liczby oprócz 1 i siebie. Na przykład, liczba 4 ma dzielniki 1, 2 i 4, więc jest liczbą złożoną. Liczby pierwsze odgrywają kluczową rolę w teorii liczb, ponieważ są podstawowymi "klockami" budującymi inne liczby.
Przykłady liczb pierwszych i ich znaczenie w kryptografii
Liczby pierwsze są niezwykle ważne w kryptografii, dziedzinie zajmującej się zabezpieczaniem informacji. Na przykład, liczba 2 jest jedyną liczbą parzystą, która jest liczbą pierwszą. W kryptografii, liczby pierwsze są wykorzystywane w algorytmach, takich jak RSA, które zapewniają bezpieczeństwo przesyłanych danych w Internecie. Inne liczby pierwsze, takie jak 3, 5 i 7, również mają swoje zastosowanie w różnych metodach szyfrowania.
W praktyce, kluczowe znaczenie liczb pierwszych polega na tym, że są one trudne do rozłożenia na czynniki, co czyni je idealnymi do tworzenia kluczy szyfrujących. Na przykład, w algorytmie RSA, dwa duże liczby pierwsze są mnożone, aby stworzyć klucz publiczny, a ich rozkładanie na czynniki jest bardzo trudne, co zapewnia bezpieczeństwo. Poniżej znajduje się tabela z przykładowymi liczbami pierwszymi oraz ich zastosowaniami w różnych algorytmach szyfrowania.
| Liczba pierwsza | Zastosowanie |
| 2 | Podstawowy element w algorytmach kryptograficznych |
| 3 | Używana w niektórych metodach szyfrowania |
| 5 | Wykorzystywana w algorytmach klucza publicznego |
| 7 | Używana w systemach szyfrowania |
Nowe kierunki w zastosowaniach liczb pierwszych w technologii
W miarę jak technologia rozwija się, liczby pierwsze stają się kluczowym elementem nie tylko w kryptografii, ale także w technologii blockchain oraz w algorytmach sztucznej inteligencji. W blockchainie, liczby pierwsze są wykorzystywane do tworzenia unikalnych identyfikatorów, które zapewniają bezpieczeństwo transakcji. Ich właściwości, takie jak trudność w rozkładzie na czynniki, sprawiają, że są idealne do generowania kluczy publicznych, co jest niezbędne w systemach opartych na decentralizacji.
Dodatkowo, liczby pierwsze są wykorzystywane w algorytmach uczenia maszynowego, gdzie pomagają w optymalizacji procesów obliczeniowych. Na przykład, w niektórych technikach kompresji danych, liczby pierwsze mogą być używane do szybkiego rozwiązywania problemów związanych z analizą zbiorów danych. W przyszłości możemy spodziewać się, że liczby pierwsze będą odgrywać jeszcze większą rolę w nowych technologiach, takich jak kwantowa kryptografia, gdzie ich unikalne właściwości będą kluczowe dla zapewnienia bezpieczeństwa w erze komputerów kwantowych.