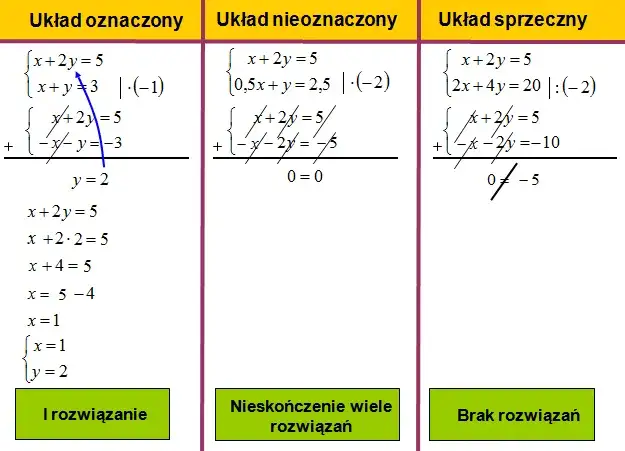
Kiedy równanie ma nieskończenie wiele rozwiązań? To pytanie nurtuje wielu uczniów i studentów matematyki. Równanie ma nieskończoną liczbę rozwiązań, gdy po jego uproszczeniu uzyskujemy tożsamość, co oznacza, że jest ono prawdziwe dla każdej wartości zmiennej. Przykładem może być równanie, które po przekształceniu przyjmuje postać $$0=0$$, co wskazuje, że każda liczba podstawiona pod niewiadomą spełnia równanie.
W artykule przyjrzymy się warunkom, które prowadzą do nieskończonej liczby rozwiązań, analizując zarówno równania liniowe, jak i kwadratowe. Zrozumienie tych zasad jest kluczowe, aby móc skutecznie rozwiązywać problemy matematyczne oraz interpretować układy równań w kontekście graficznym.
Kluczowe informacje:
- Nieskończona liczba rozwiązań występuje, gdy równanie po uproszczeniu staje się tożsamością.
- Równania liniowe mają nieskończoną liczbę rozwiązań, gdy współczynniki i wyrazy wolne są identyczne po obu stronach.
- Równania kwadratowe również mogą mieć nieskończoną liczbę rozwiązań, co wymaga szczegółowej analizy.
- Tożsamości matematyczne odgrywają kluczową rolę w zrozumieniu nieskończonej liczby rozwiązań.
- W układach równań nieskończona liczba rozwiązań występuje, gdy proste reprezentujące równania pokrywają się.
Zrozumienie nieskończonej liczby rozwiązań w równaniach
Równanie ma nieskończoną liczbę rozwiązań, gdy po jego uproszczeniu uzyskujemy tożsamość, co oznacza, że jest ono prawdziwe dla każdej wartości zmiennej. Tego typu równania są istotne w matematyce, ponieważ pokazują, że istnieje wiele wartości, które spełniają dane równanie. W praktyce, gdy równanie prowadzi do postaci, takiej jak $$0=0$$, każda liczba podstawiona pod niewiadomą spełnia równanie, co jest kluczowym aspektem w analizie równań.
W kontekście algebraicznym, nieskończona liczba rozwiązań jest ważna, ponieważ umożliwia zrozumienie, jak różne równania mogą się ze sobą łączyć. W przypadku równań liniowych, takie sytuacje występują, gdy współczynniki przy zmiennej oraz wyrazy wolne po obu stronach równania są identyczne. To zjawisko jest fundamentalne dla analizy rozwiązań w matematyce i ma zastosowanie w różnych dziedzinach, od inżynierii po ekonomię.
Co to znaczy, że równanie ma nieskończenie wiele rozwiązań?
Gdy mówimy, że równanie ma nieskończoną liczbę rozwiązań, odnosimy się do sytuacji, w której równanie staje się tożsamością. Oznacza to, że po przekształceniach algebraicznych uzyskujemy równanie, które jest zawsze prawdziwe, niezależnie od wartości zmiennej. Przykładowo, równanie $$2x + 3 = 2x + 3$$ jest tożsamością, ponieważ obie strony są identyczne.
Tożsamości w matematyce są kluczowe, ponieważ pomagają nam zrozumieć, jak różne równania mogą być ze sobą powiązane. Kiedy równanie przyjmuje formę tożsamości, wskazuje to na nieskończoną liczbę rozwiązań, co jest ważnym aspektem w rozwiązywaniu problemów matematycznych. W praktyce, każda liczba, którą podstawimy pod zmienną, będzie spełniać takie równanie, co czyni je niezwykle użytecznym w analizie matematycznej.
Jakie są warunki, aby równanie miało nieskończoną liczbę rozwiązań?
Aby równanie miało nieskończoną liczbę rozwiązań, muszą być spełnione określone warunki. Przede wszystkim, współczynniki przy zmiennej oraz wyrazy wolne muszą być identyczne po obu stronach równania. Taka sytuacja prowadzi do powstania tożsamości, co oznacza, że równanie jest prawdziwe dla każdej wartości zmiennej. Na przykład, jeśli uprościmy równanie do formy $$0=0$$, potwierdzamy, że każda liczba podstawiona pod zmienną spełnia to równanie.
Kolejnym warunkiem jest, że podczas przekształcania równania nie może dojść do utraty informacji, co oznacza, że wszystkie operacje muszą być zgodne z zasadami algebraicznymi. W przeciwnym razie, równanie może stać się sprzeczne, co prowadzi do ograniczonej liczby rozwiązań. W przypadku układów równań, nieskończona liczba rozwiązań występuje, gdy proste reprezentujące te równania pokrywają się, co również wskazuje na identyczność ich współczynników.
Analiza równań liniowych z nieskończoną liczbą rozwiązań
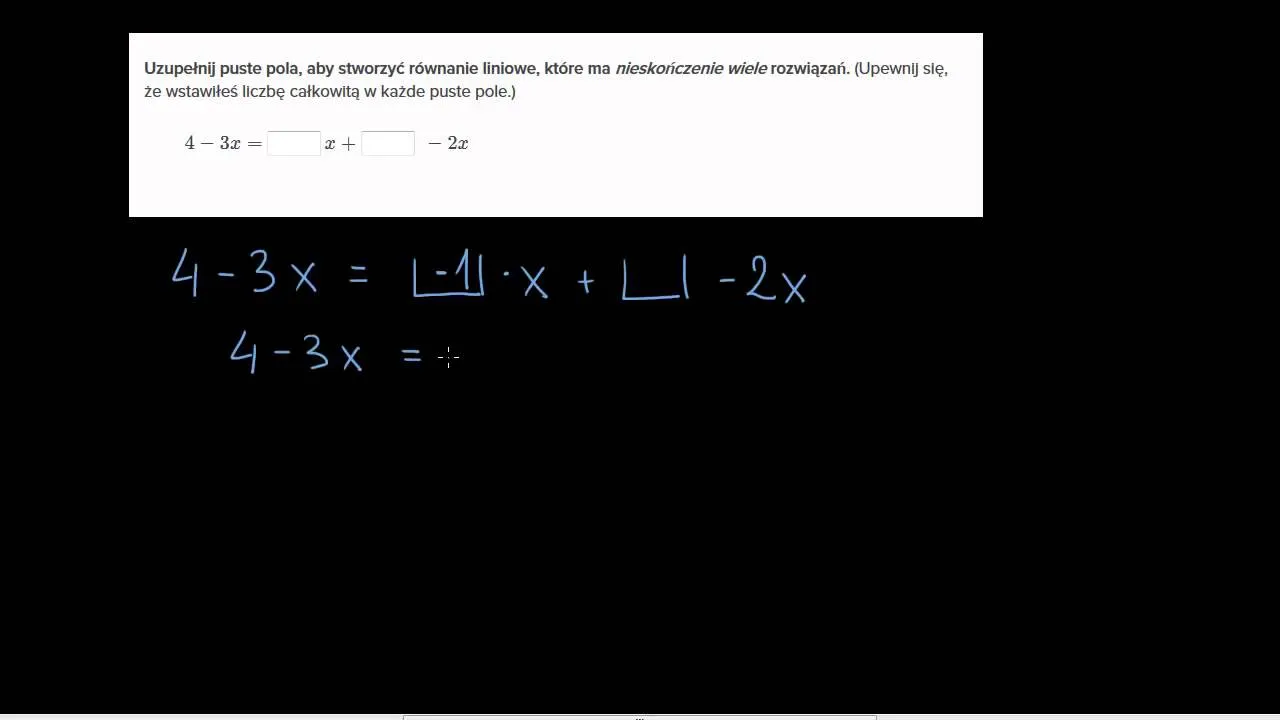
Równania liniowe mogą mieć nieskończoną liczbę rozwiązań, gdy obie strony równania są identyczne, co prowadzi do tożsamości algebraicznej. Na przykład, równanie $$2x + 3 = 2x + 3$$ jest doskonałym przykładem, ponieważ po uproszczeniu obie strony pozostają takie same, co oznacza, że każda wartość zmiennej x spełnia to równanie. Innym przykładem jest równanie $$4x + 3 + 5x = 3(3x + 1)$$, które po uproszczeniu prowadzi do $$9x + 3 = 9x + 3$$, co również daje tożsamość $$0=0$$.
Równania liniowe z nieskończoną liczbą rozwiązań pokazują, jak ważne jest zrozumienie relacji między współczynnikami i wyrazami wolnymi. W praktyce, jeśli równanie jest uproszczone do postaci, w której obie strony są identyczne, to każde x będzie rozwiązaniem. Takie równania są istotne w różnych dziedzinach, od inżynierii po ekonomię, ponieważ pozwalają na elastyczność w rozwiązaniach.
| Forma równania | Uproszczona forma |
|---|---|
| 2x + 3 = 2x + 3 | 0 = 0 |
| 4x + 3 + 5x = 3(3x + 1) | 0 = 0 |
| 6x - 2 = 2(3x - 1) | 0 = 0 |
Równania kwadratowe i ich nieskończone rozwiązania
Równania kwadratowe również mogą mieć nieskończoną liczbę rozwiązań, choć jest to mniej powszechne niż w przypadku równań liniowych. Przykładem takiego równania jest $$x^2 - 4 = 0$$, które po przekształceniu do postaci $$x^2 - 4 = (x - 2)(x + 2)$$ ma dwa rozwiązania, ale jeśli zmienimy równanie na $$x^2 - 4x + 4 = 0$$, to uproszczone do $$0 = 0$$ wskazuje, że wszystkie wartości x spełniają to równanie. To pokazuje, że w pewnych warunkach, równania kwadratowe mogą prowadzić do nieskończonej liczby rozwiązań.
Warto zauważyć, że aby równanie kwadratowe miało nieskończoną liczbę rozwiązań, musi być tożsamością, co oznacza, że wszystkie współczynniki muszą być identyczne w obu stronach równania. Takie przypadki są rzadziej spotykane, ale są ważne w kontekście analizy równań i ich zastosowań w praktyce.
Tożsamości i równania równoważne w kontekście rozwiązań
Tożsamości oraz równania równoważne odgrywają kluczową rolę w zrozumieniu, kiedy równanie ma nieskończenie wiele rozwiązań. Gdy równanie staje się tożsamością, oznacza to, że jest prawdziwe dla każdej wartości zmiennej, co prowadzi do nieskończonej liczby rozwiązań. W praktyce, identyfikacja tożsamości pozwala na uproszczenie równań oraz lepsze zrozumienie ich struktury. Równania równoważne są natomiast równaniami, które mają tę samą wartość dla wszystkich zmiennych, mimo że mogą wyglądać inaczej. Zrozumienie tych pojęć jest kluczowe dla analizy równań i ich zastosowań w różnych dziedzinach matematyki.
Jak tożsamości wpływają na nieskończoną liczbę rozwiązań?
Tożsamości mają istotny wpływ na nieskończoną liczbę rozwiązań, ponieważ wskazują na sytuacje, w których równanie jest zawsze prawdziwe. Gdy równanie po uproszczeniu przyjmuje formę tożsamości, takiej jak $$0=0$$, każda wartość zmiennej będzie spełniać to równanie. Tożsamości są zatem podstawą do zrozumienia, dlaczego niektóre równania mają nieskończoną liczbę rozwiązań. W kontekście analizy algebraicznej, umiejętność rozpoznawania tożsamości pozwala na efektywne rozwiązywanie problemów matematycznych oraz zastosowanie ich w praktyce, co czyni je niezwykle wartościowymi w edukacji matematycznej.
Rola równań równoważnych w znajdowaniu rozwiązań
Równania równoważne są kluczowe w procesie znajdowania nieskończonej liczby rozwiązań. Dwa równania są równoważne, jeśli mają tę samą wartość dla wszystkich zmiennych, co oznacza, że można je przekształcać bez utraty ich znaczenia. Umożliwia to uproszczenie skomplikowanych równań do form, które są łatwiejsze do analizy. Dzięki temu, można łatwiej identyfikować warunki, które prowadzą do nieskończonej liczby rozwiązań. Zrozumienie i umiejętność pracy z równaniami równoważnymi jest niezbędne w matematyce, szczególnie w kontekście rozwiązywania równań liniowych i układów równań.
Czytaj więcej: Jak się mnoży logarytmy - proste zasady i najczęstsze błędy
Układy równań a nieskończona liczba rozwiązań
Układy równań mogą również prowadzić do nieskończonej liczby rozwiązań, gdy proste reprezentujące te równania pokrywają się w przestrzeni. W takich przypadkach, każdy punkt na tej prostej jest rozwiązaniem układu, co oznacza, że istnieje nieskończona liczba wartości, które spełniają te równania. Zrozumienie tego zjawiska jest istotne, ponieważ pozwala na lepsze analizowanie i rozwiązywanie problemów matematycznych w różnych kontekstach, zarówno w teorii, jak i w praktyce. Graficzne przedstawienie układów równań może pomóc w wizualizacji, jak te proste się pokrywają, co jest kluczowe dla zrozumienia, dlaczego pewne układy mają nieskończoną liczbę rozwiązań.
Praktyczne zastosowania nieskończonej liczby rozwiązań w inżynierii
W kontekście inżynierii, zrozumienie nieskończonej liczby rozwiązań ma kluczowe znaczenie dla projektowania systemów i analizowania ich funkcjonowania. Na przykład, w inżynierii strukturalnej, równania równoważne mogą być wykorzystywane do modelowania zachowań materiałów pod różnymi obciążeniami. Dzięki umiejętności identyfikacji tożsamości i równania równoważne, inżynierowie mogą optymalizować projekty, aby zapewnić maksymalną efektywność i bezpieczeństwo, minimalizując jednocześnie koszty.
Dodatkowo, w obszarze analizy danych, umiejętność pracy z równaniami o nieskończonej liczbie rozwiązań otwiera nowe możliwości w zakresie modelowania złożonych systemów. Wykorzystując zaawansowane techniki, takie jak analiza wielowymiarowa i symulacje komputerowe, specjaliści mogą przewidywać zachowania systemów w warunkach rzeczywistych, co ma zastosowanie w różnych dziedzinach, od ekonomii po biotechnologię. Te podejścia nie tylko zwiększają precyzję analiz, ale również pozwalają na testowanie hipotez w sposób, który byłby niemożliwy przy użyciu tradycyjnych metod.