Okres w matematyce to kluczowe pojęcie, które odnosi się do powtarzających się elementów w różnych kontekstach. W szczególności, okres może dotyczyć zarówno ułamków dziesiętnych, jak i funkcji matematycznych. W przypadku ułamków okresowych, mamy do czynienia z nieskończonym ciągiem cyfr po przecinku, który powtarza się w sposób cykliczny. Przykładem może być liczba $$0,(3)$$, co oznacza $$0,333...$$. Z drugiej strony, funkcje okresowe to funkcje, których wartości powtarzają się w regularnych odstępach, co jest istotne przy modelowaniu zjawisk cyklicznych, takich jak fale czy ruch wahadła.
Zrozumienie tych pojęć jest niezbędne dla każdego, kto pragnie zgłębić matematykę. W artykule omówimy, jak definiuje się okres w matematyce, przedstawimy przykłady ułamków okresowych oraz funkcji okresowych, a także ich zastosowania w praktyce. Przyjrzymy się także wizualizacji tych koncepcji, co pomoże lepiej zrozumieć ich znaczenie.
Najistotniejsze informacje:
- Okres w matematyce odnosi się do powtarzającej się grupy cyfr w ułamkach dziesiętnych oraz do stałych odstępów w funkcjach okresowych.
- Ułamki okresowe mają nieskończone rozwinięcie, które można przedstawić w postaci ułamka zwykłego.
- Funkcje okresowe, takie jak sinus, mają stały okres, co pozwala na modelowanie zjawisk cyklicznych.
- Wizualizacja okresów w funkcjach matematycznych jest kluczowa dla ich zrozumienia, a grafy pomagają w interpretacji danych.
- Okresowe funkcje i ułamki okresowe znajdują zastosowanie w różnych dziedzinach, od finansów po nauki przyrodnicze.
Jak definiuje się okres w matematyce i jego znaczenie?
Pojęcie okresu w matematyce odnosi się do powtarzającej się grupy cyfr w rozwinięciu dziesiętnym ułamka nieskończonego, znanego jako ułamek okresowy. Jest to kluczowy element w zrozumieniu, jak różne liczby mogą być reprezentowane w formie dziesiętnej. Okres ma także istotne znaczenie w kontekście funkcji okresowych, które są używane do modelowania zjawisk cyklicznych, takich jak fale czy ruch wahadła. Wartości funkcji okresowych powtarzają się w regularnych odstępach, co czyni je bardzo przydatnymi w matematyce i naukach przyrodniczych.
W kontekście ułamków dziesiętnych, okres to nieskończony, powtarzający się ciąg cyfr po przecinku, który jest zapisywany w nawiasie. Na przykład, liczba $$0,(3)$$ oznacza $$0,333...$$, co wskazuje na to, że cykl powtarza się w nieskończoność. Ułamek dziesiętny okresowy można przedstawić w postaci ułamka zwykłego, co jest kluczowe dla zrozumienia, jak operować na takich liczbach w praktyce. W polskiej notacji okres zapisuje się w nawiasie, natomiast w anglojęzycznej literaturze stosuje się nadkreślenie.
Zrozumienie pojęcia okresu w ułamkach dziesiętnych
Ułamek okresowy to liczba, która ma powtarzający się ciąg cyfr po przecinku. Na przykład, $$\frac{1}{3}$$ jest reprezentowany jako $$0,(3)$$, co oznacza, że liczba 3 powtarza się w nieskończoność. Istnieją również ułamki okresowe z przedokresem, które mają skończoną liczbę cyfr przed okresem, jak w przypadku $$0,1(2)$$, co oznacza $$0,1222...$$. Tego typu reprezentacje są nie tylko interesujące z matematycznego punktu widzenia, ale także mają praktyczne zastosowanie w codziennym życiu.
Ważne jest, aby zrozumieć, jak okres w ułamkach dziesiętnych wpływa na obliczenia matematyczne oraz jak można je wykorzystywać w różnych kontekstach. Ułatwia to pracę z liczbami, które w przeciwnym razie mogłyby wydawać się skomplikowane. Przy odpowiednim zrozumieniu, można z łatwością przekształcać te liczby w inne formy, co jest kluczowe w wielu dziedzinach, takich jak finanse czy inżynieria.
| Ułamek dziesiętny | Ułamek zwykły |
| 0,333... | 1/3 |
| 0,142857... | 1/7 |
| 0,1(2) | 1/8 |
Czym są funkcje okresowe i ich właściwości?
Funkcje okresowe to takie funkcje matematyczne, które mają powtarzający się wzór w regularnych odstępach czasu. Oznacza to, że dla każdej wartości x w dziedzinie funkcji, zachodzi równość $$f(x + T) = f(x)$$, gdzie T to okres funkcji. Funkcje te są niezwykle ważne w matematyce, ponieważ pozwalają na modelowanie zjawisk cyklicznych, takich jak fale dźwiękowe, ruch wahadła czy zmiany pór roku. Właściwości funkcji okresowych są szeroko stosowane w różnych dziedzinach, w tym w fizyce, inżynierii i ekonomii.
Znajomość funkcji okresowych jest kluczowa, ponieważ umożliwia analizę i przewidywanie zachowań systemów, które wykazują cykliczność. Przykłady zastosowań obejmują analizę drgań w mechanice, modelowanie fal w akustyce oraz badanie cykli ekonomicznych. Właściwości funkcji okresowych, takie jak amplituda, częstotliwość i faza, są istotne dla zrozumienia, jak te funkcje działają w praktyce.
Definicja funkcji okresowej i jej zastosowania
Funkcja okresowa to funkcja, która powtarza swoje wartości w regularnych odstępach. W praktyce oznacza to, że po upływie określonego czasu, wartości funkcji wracają do tych samych punktów. Dla przykładu, funkcja sinusoidalna jest jedną z najbardziej znanych funkcji okresowych, która ma okres równy $$2\pi$$. Dzięki tej właściwości, funkcje okresowe są niezwykle przydatne w różnych dziedzinach, takich jak inżynieria czy fizyka, gdzie modelują zjawiska takie jak fale dźwiękowe czy elektromagnetyczne.
W inżynierii, funkcje okresowe są używane do analizy drgań i sygnałów. Na przykład, w telekomunikacji, fale radiowe są reprezentowane przez funkcje okresowe, co pozwala na przesyłanie informacji na dużą odległość. W fizyce, funkcje te pomagają w opisie ruchu wahadeł oraz innych systemów dynamicznych. Ich zastosowanie w różnych dziedzinach pokazuje, jak ważne jest zrozumienie ich właściwości.- Modelowanie fal dźwiękowych w akustyce.
- Analiza drgań w mechanice i inżynierii.
- Badanie cykli ekonomicznych w ekonomii.
Czytaj więcej: Jak się mnoży logarytmy - proste zasady i najczęstsze błędy
Jak wizualizować okres w funkcjach matematycznych?
Wizualizacja okresu w funkcjach matematycznych jest kluczowa dla zrozumienia ich zachowania i właściwości. Graficzne przedstawienie funkcji okresowych pozwala na łatwe zauważenie powtarzalności wartości, co jest istotne w analizie cyklicznych zjawisk. Dzięki wykresom można dostrzegać nie tylko okres, ale również amplitudę i fazę funkcji, co ułatwia interpretację danych. Wizualizacja pomaga również w nauczaniu, ponieważ obrazy często są bardziej zrozumiałe niż same liczby czy wzory matematyczne.
W przypadku funkcji okresowych, takich jak sinus czy cosinus, wykresy mają charakterystyczne kształty, które można łatwo rozpoznać. Analizując te wykresy, można określić, jak długo trwa jeden cykl oraz jakie są maksymalne i minimalne wartości funkcji. To zrozumienie jest niezbędne w wielu dziedzinach, takich jak inżynieria, akustyka czy fizyka, gdzie cykliczność zjawisk odgrywa kluczową rolę.
Grafy funkcji okresowych i ich interpretacja
Grafy funkcji okresowych pozwalają na identyfikację istotnych właściwości, takich jak okres i amplituda. Okres funkcji to odległość na osi poziomej (x), po której wartości funkcji się powtarzają. Na przykład, w przypadku funkcji sinus, okres wynosi $$2\pi$$, co oznacza, że po przebyciu tej odległości na osi x, wartości funkcji wracają do tych samych punktów. Amplituda, z kolei, to maksymalna wartość funkcji, która wskazuje, jak daleko funkcja sięga powyżej lub poniżej osi poziomej.
Interpretacja grafów funkcji okresowych jest kluczowa w analizie zjawisk cyklicznych. Dzięki wykresom można łatwo zauważyć zmiany w zachowaniu funkcji, co pozwala na lepsze zrozumienie ich dynamiki. W kontekście praktycznym, analiza wykresów jest niezbędna w takich dziedzinach jak analiza sygnałów, gdzie dokładne odczyty wartości są kluczowe dla skutecznego działania systemów technologicznych.
- Okres funkcji można zidentyfikować jako długość jednego cyklu na wykresie.
- Amplituda wskazuje maksymalną wartość funkcji w stosunku do osi poziomej.
- Wizualizacja pozwala na szybką interpretację danych i identyfikację wzorców.
Wpływ częstotliwości na kształt funkcji okresowych
Częstotliwość ma kluczowy wpływ na kształt i charakterystykę funkcji okresowych. Im wyższa częstotliwość, tym krótszy okres funkcji, co oznacza, że wartości funkcji zmieniają się szybciej. Na przykład, w funkcji sinus, zwiększenie częstotliwości powoduje, że wykres staje się bardziej „ściśnięty”, a cykle powtarzają się w krótszym czasie. W praktyce oznacza to, że dla wyższych częstotliwości amplituda może wydawać się mniej wyraźna, ponieważ zmiany zachodzą w krótszym czasie, co wpływa na interpretację danych.
Warto zauważyć, że częstotliwość nie tylko wpływa na szybkość zmian wartości funkcji, ale również na jej zastosowanie w różnych dziedzinach. W inżynierii dźwięku, na przykład, różne częstotliwości odpowiadają różnym tonom muzycznym. Wysokie częstotliwości są związane z wyższymi dźwiękami, natomiast niskie częstotliwości odpowiadają dźwiękom basowym. Zrozumienie tej zależności jest kluczowe dla inżynierów dźwięku i muzyków, którzy muszą precyzyjnie kontrolować, jak dźwięki są produkowane i przetwarzane.
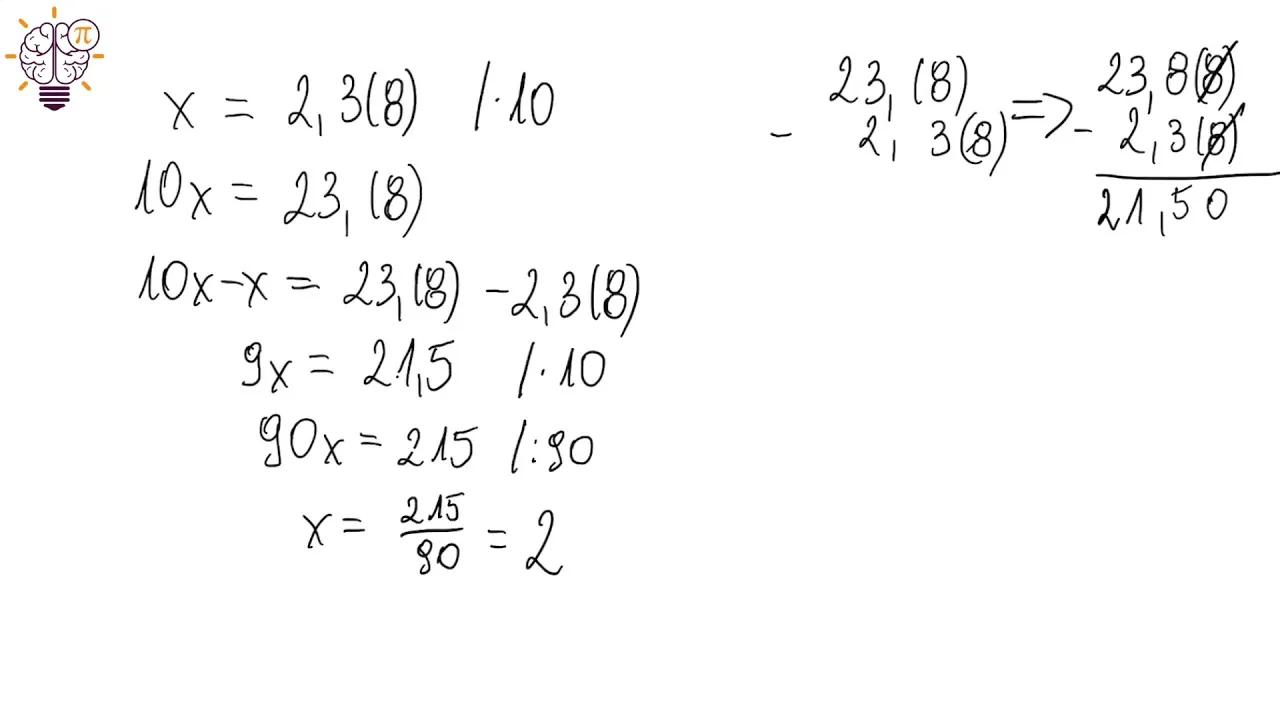
Zastosowania okresów w praktycznych problemach matematycznych
Okresy w matematyce mają wiele praktycznych zastosowań, które są istotne w różnych dziedzinach życia. Na przykład, w fizyce, funkcje okresowe są używane do modelowania ruchu fal, co jest kluczowe w akustyce i optyce. W ekonomii, cykle gospodarcze mogą być analizowane za pomocą funkcji okresowych, co pozwala na przewidywanie trendów rynkowych. Ponadto, w inżynierii, zrozumienie okresów i częstotliwości jest niezbędne do projektowania systemów, takich jak silniki czy urządzenia elektroniczne, które muszą działać w określonych cyklach.
Przykłady zastosowań obejmują również analizę sygnałów w telekomunikacji, gdzie funkcje okresowe pomagają w przesyłaniu danych. W medycynie, funkcje okresowe są wykorzystywane do analizy rytmów biologicznych, takich jak rytmy serca czy cykle snu. Dzięki tym zastosowaniom, okres w matematyce staje się nie tylko teoretycznym pojęciem, ale także praktycznym narzędziem do rozwiązywania realnych problemów.
Jak okresowe funkcje modelują zjawiska w rzeczywistości?
Funkcje okresowe są niezwykle użyteczne w modelowaniu różnych zjawisk w rzeczywistości. Na przykład, fale dźwiękowe są doskonałym przykładem zastosowania funkcji sinusoidalnej. W akustyce, częstotliwość fali dźwiękowej decyduje o tonie, który słyszymy. Wysokie częstotliwości odpowiadają wyższym dźwiękom, podczas gdy niskie częstotliwości dają dźwięki basowe. Dzięki funkcjom okresowym możemy dokładnie opisać, jak dźwięki rozprzestrzeniają się w powietrzu oraz jak różne instrumenty muzyczne generują różne tony.
Innym przykładem są fale elektromagnetyczne, które również można modelować za pomocą funkcji okresowych. W przypadku światła, różne długości fal odpowiadają różnym kolorom. Na przykład, niebieskie światło ma krótszą długość fali, podczas gdy czerwone ma dłuższą. Zrozumienie tych zjawisk jest kluczowe w dziedzinach takich jak optyka czy telekomunikacja, gdzie funkcje okresowe pomagają w analizie i projektowaniu systemów przesyłania informacji.
Przykłady zastosowań ułamków okresowych w codziennym życiu
Ułamki okresowe znajdują szerokie zastosowanie w codziennych obliczeniach, zwłaszcza w finansach. Na przykład, obliczając odsetki od kredytów czy lokat, często napotykamy na wartości, które można przedstawić jako ułamki okresowe. Przykładem może być oprocentowanie wynoszące 3,333...%, co w praktyce oznacza, że odsetki będą się powtarzać w cyklu. Dzięki zastosowaniu ułamków okresowych, obliczenia stają się prostsze i bardziej zrozumiałe.
Kolejnym zastosowaniem ułamków okresowych jest pomiar czasu. Na przykład, w kontekście cykli biologicznych, takich jak rytm serca, wartości mogą być przedstawione jako ułamki dziesiętne okresowe, co ułatwia lekarzom analizę i interpretację wyników badań. Użycie ułamków okresowych w takich sytuacjach pozwala na dokładniejsze pomiary i lepsze zrozumienie zjawisk, które mają miejsce w organizmach żywych.
- Obliczanie odsetek kredytów i lokat.
- Analiza rytmów biologicznych, takich jak rytm serca.
- Ustalanie cen produktów w handlu, gdzie ceny mogą mieć wartości okresowe.
Jak wykorzystać okresowe funkcje w technologii i sztucznej inteligencji?
W miarę jak technologia i sztuczna inteligencja rozwijają się, funkcje okresowe stają się coraz bardziej istotne w analizie danych i modelowaniu zjawisk. Na przykład, w uczeniu maszynowym, algorytmy mogą wykorzystywać funkcje okresowe do rozpoznawania wzorców w dużych zbiorach danych, takich jak analiza zachowań użytkowników w aplikacjach mobilnych czy przewidywanie trendów rynkowych. Dzięki zrozumieniu i zastosowaniu tych funkcji, inżynierowie mogą tworzyć bardziej efektywne modele predykcyjne, które lepiej oddają cykliczność danych.
Dodatkowo, w kontekście Internetu Rzeczy (IoT), funkcje okresowe mogą być używane do monitorowania i optymalizacji procesów w czasie rzeczywistym. Na przykład, czujniki mogą zbierać dane o temperaturze, wilgotności czy ciśnieniu atmosferycznym, a ich wartości mogą być analizowane jako funkcje okresowe. Umożliwia to automatyczne dostosowywanie systemów, takich jak ogrzewanie czy klimatyzacja, w odpowiedzi na zmieniające się warunki, co prowadzi do większej efektywności energetycznej i oszczędności kosztów. W ten sposób, zastosowanie funkcji okresowych w nowoczesnych technologiach może przynieść znaczące korzyści zarówno w codziennym życiu, jak i w przemyśle.

